Appearance
平衡二叉树 (AVL)
AVL树
AVL树,又称为平衡二叉树,它是一种特殊的二叉查找树(Binary Search Tree, BST),其每一个节点的左右子树的高度差不超过1。
平衡二叉树递归定义如下:
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
介绍
在二叉搜索树的那一节里,我们在最后提到了如果二叉树严重不平衡,其时间复杂度会退化到线性的复杂度,例如从有序数组[1, 2, 3, 4, 5]中构建出的二叉树,就会成为一个线性表,如下图所示。
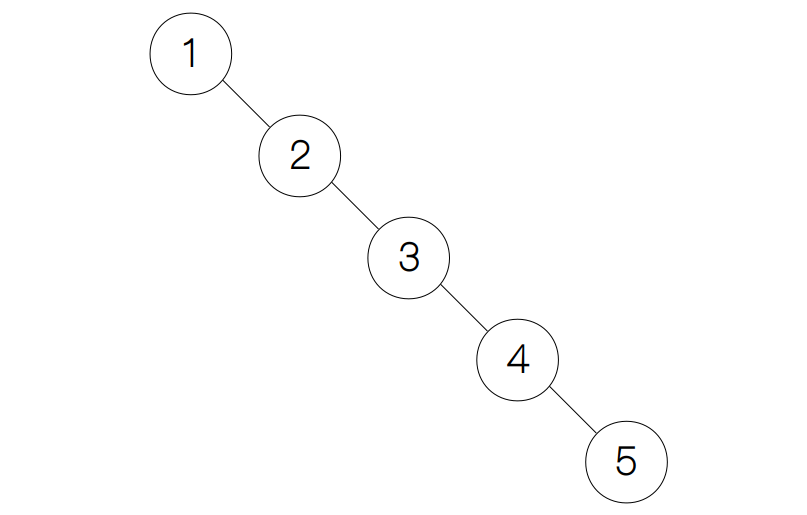
因此,我们需要有一棵能够自动平衡的二叉树,使得每次插入、删除和查找的复杂度都接近 Θ(nlog n) 的复杂度。AVL 树就是最早被提出的自平衡二叉搜索树,它是由两名俄国的科学家(G. M. Adelson-Velsky 和 E. M. Landis)提出。下面,我们就来看看它是如何做到自平衡的吧。
平衡因子
AVL 树最核心的思想就是计算每个节点的平衡因子(balance factor),平衡因子的定义是一个节点的左孩子的高度减去其右孩子的高度。这里的高度(height)就是指从一个节点出发到达最远叶子节点所经过的最长路径,例如下图的例子中节点 3 到达最远的叶子节点 2 所需要经过的路径长度为 2(从节点 3 到节点 1 和 从节点 1 到节点 2)。
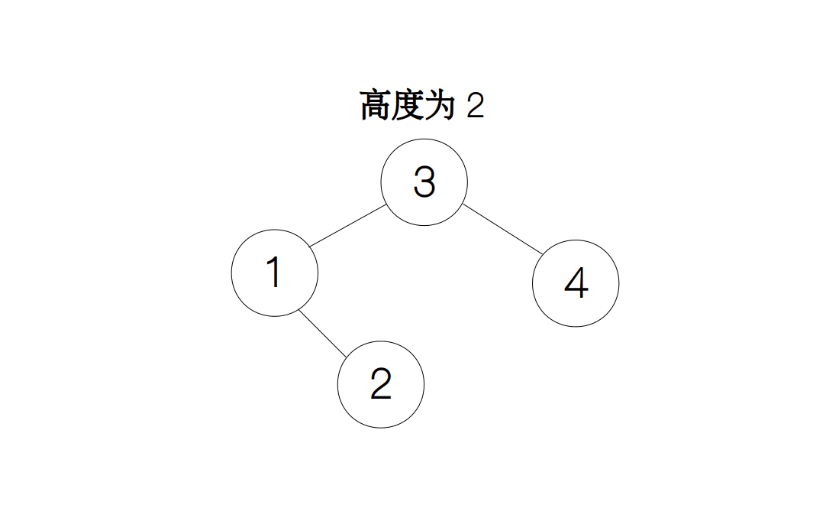
AVL 树最核心的思想就是计算每个节点的平衡因子(balance factor),平衡因子的定义是一个节点的左孩子的高度减去其右孩子的高度。这里的高度(height)就是指从一个节点出发到达最远叶子节点所经过的最长路径,例如下图的例子中节点 3 到达最远的叶子节点 2 所需要经过的路径长度为 2(从节点 3 到节点 1 和 从节点 1 到节点 2)。
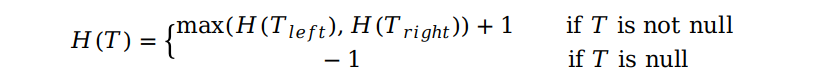
例如,下图中的两个例子,根节点的平衡因子分别为 2 和 -2。

旋转操作
从前面的例子中,我们发现当一个节点的平衡因子的绝对值大于等于 2 时,树就不再平衡。这里,AVL 树提供了一种旋转机制,使得旋转过后的树不仅能保持二叉搜索树的性质,同时能够使节点的平衡因子的绝对值小于 2,接下来我们就分别来讨论一下不同情况下的旋转操作。
LL 型
下图表示的是 LL 型的情况,在根节点的左孩子的左侧添加新节点 1 后,平衡因子从原来的 1 变为了 2,这时我们只需要对根节点 3 执行一次右旋操作树就平衡了。
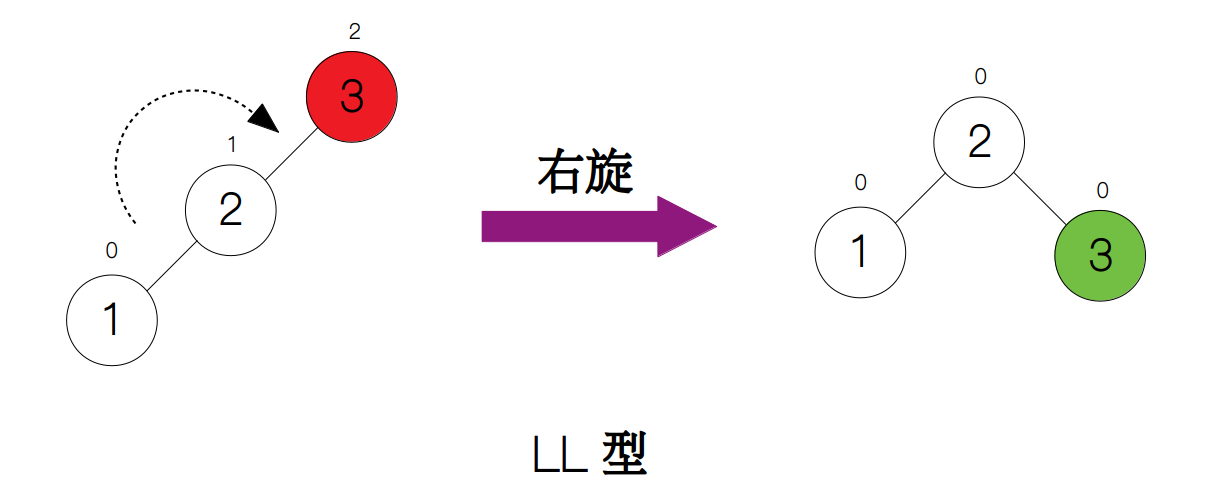
LR 型
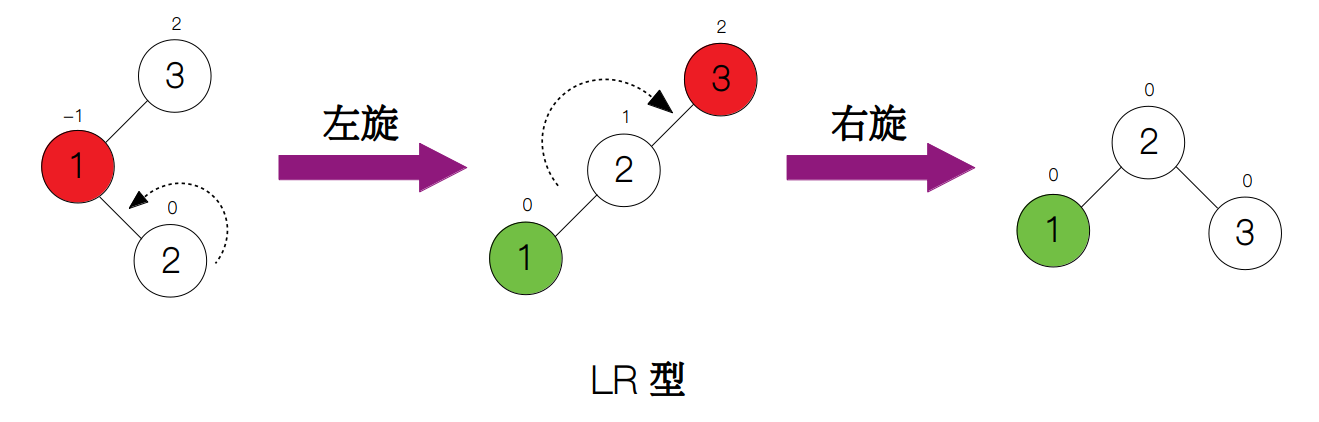
如果往根节点的左孩子的右侧添加新节点(下图中的节点 2),平衡因子也会从 1 变为 2,但这里我们不能采用单次右旋,而是要先对根节点的左孩子执行一次左旋操作,使之变为 LL 型,然后再对根节点进行右旋。
RR 型
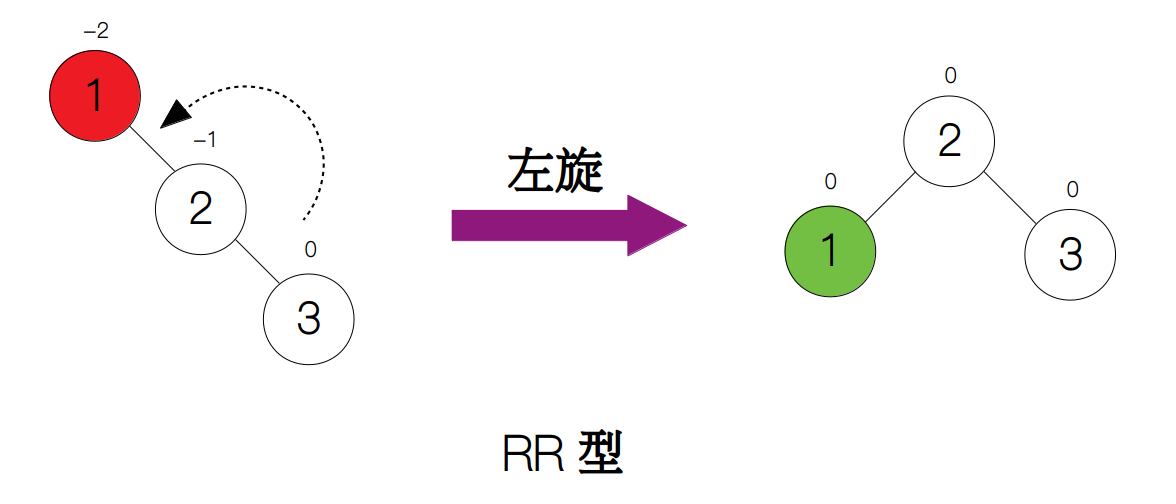
RR 型正好与 LL 型的互为镜像,如果向根节点的右孩子的右侧添加一个新节点(下图中的节点 3)后,平衡因子由 -1 变为 -2,导致树的不平衡,这时我们需要对根节点执行一次左旋操作。
RL 型
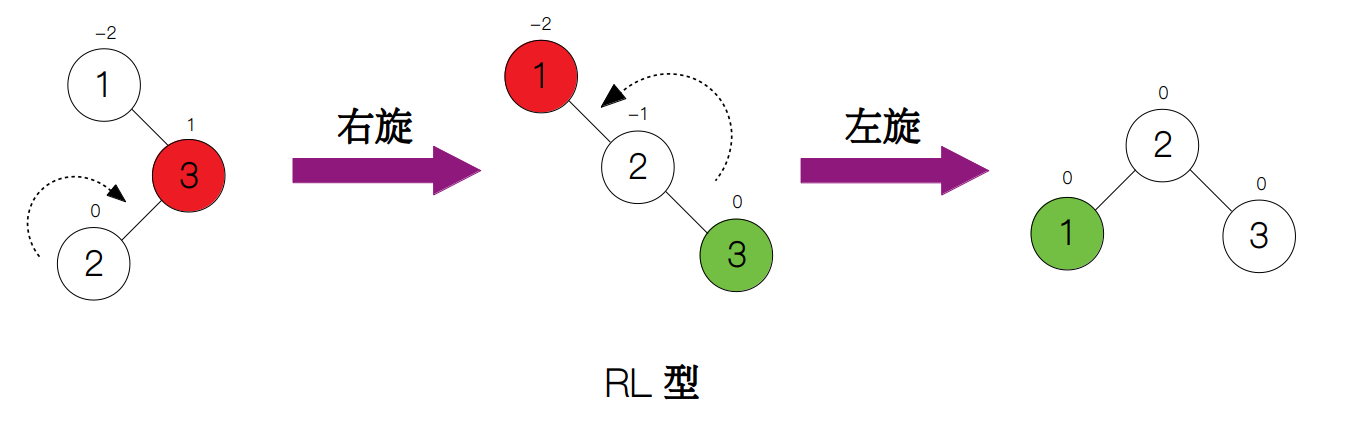
RL 型与 LR 型也互为镜像,即如果将新节点(下图中的节点 2)插入到根节点的右孩子的左侧,平衡因子由 -1 变为 -2。同样,我们不能用一次左旋来使树重新平衡,而是先对根节点的右孩子执行一次右旋,变为 RR 型,然后再对根节点进行左旋。
一般情况
我们看到,上述的四种情况都是基于两种基本操作:左旋和右旋。然而,我们讨论的并不是一般的情况。举个例子,如果要对下图中的根节点进行右旋,我们会发现根节点的左孩子的右子树不为空,这时该怎么办呢?我们知道,旋转之后的树必须保持二叉树的性质,所以我们可以让多余的右子树作为原根节点的左子树,使得原根节点的值还是大于被调整子树的所有节点的值。
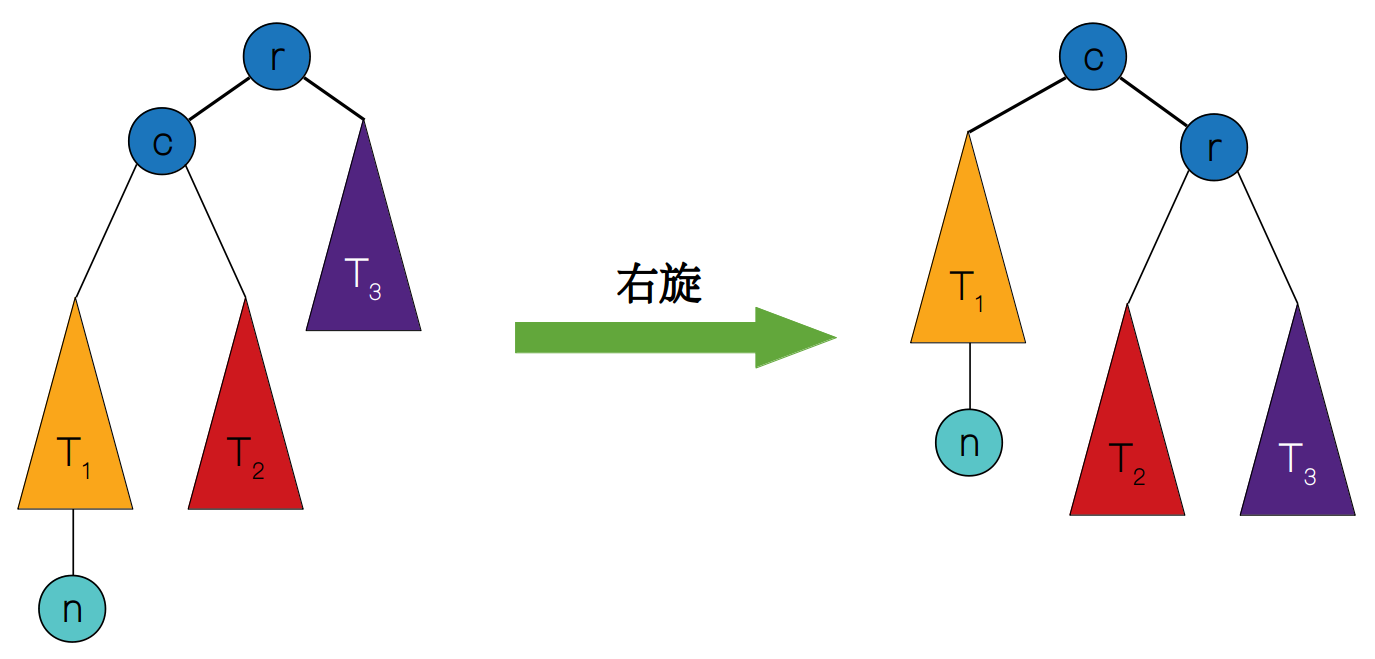
右旋的动态图可以见下图: 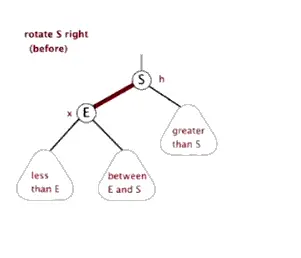
同理,下图也展示了左旋的一般情况,只是与右旋互为镜像操作。
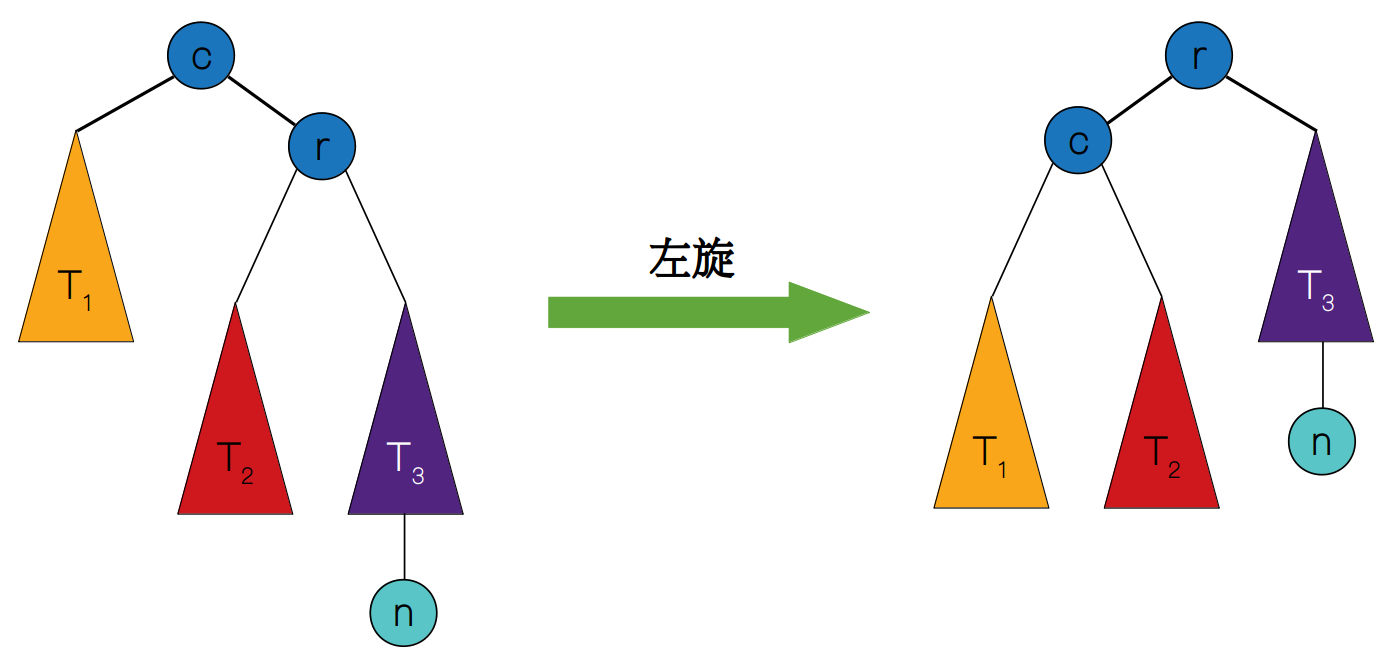
左旋的动态图可以见下图: 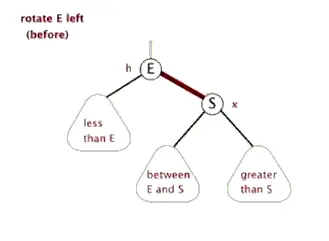
搜索
和二叉搜索树一样,AVL 树也是从根节点开始搜索,如果搜索的元素比根节点小,那么就从根节点的左子树中继续搜索,如果比根节点大,那么就从右子树中继续搜索,如果相等,则返回该节点,要是搜索到了叶子节点发现还是搜索失败,我们就返回None。
插入
AVL 树的插入操作也跟二叉搜索树一样,先找到插入的位置,即通过搜索操作找到插入位点,然后创建一个新节点,最后父节点指向该新节点。但由于 AVL 树是一棵自平衡的树,所以每插入一个节点都会更新搜索过程中所经过节点的高度,如发现有节点的高度的绝对值大于等于 2,则采取相应的旋转操作使之保持平衡。这里调用了前面写好的settle_violation函数,整个过程均采用递归的方式实现。
删除
同样,AVL 树的删除操作也类似于二叉搜索树,找到删除的节点,然后根据待删除节点的孩子节点个数,判断出该采取哪一种删除方式,由于它跟二叉搜索树一样,这里就不再赘述了,忘记了的小伙伴可以乘坐这里的传送门,找到删除操作的那一部分再看一看。与插入操作一样,删除操作也会检查搜索过程中所经过的所有节点的高度,如果其绝对值大于等于 2,我们也调用settle_violation函数来使树保持平衡,整个删除操作也是一个递归的过程。
插入和删除操作都是由查找和旋转操作构成,故两者的复杂度均为 Θ(log n) + Θ(1) = Θ(log n)。