Appearance
二叉树
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。 二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树 。
二叉树的性质
性质一:在二叉树的第i层上至多有2^(i-1)个结点(i>0)
性质二:深度为k的二叉树至多有2^k-1个结点(k>0)
性质三:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1
性质四:具有n个结点的完全二叉树的深度为floor(log2n)+1
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
国内教程定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
完全二叉树
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
性质五:如果对一棵有n个结点的完全二叉树的结点按层序编号(从第一层开始到最下一层,每一层从左到右编号),对任一结点i有:
如果i=1 ,则结点为根结点,没有双亲。
如果2 * i > n ,则结点i没有左孩子 ;否则其左孩子结点为2*i . (n为结点总数)
如果2 * i+1>n ,则结点i没有右孩子;否则其右孩子结点为2*1+1
完全二叉树的数组表示法
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些结点,将其”拼凑”成完全二叉树即可。如图 1 所示:
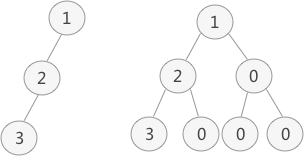
图 1 中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
解决了二叉树的转化问题,接下来学习如何顺序存储完全(满)二叉树。
完全二叉树的顺序存储,仅需从根结点开始,按照层次依次将树中结点存储到数组即可。
先序遍历
先序遍历是二叉树遍历的一种方式,它的遍历顺序是先访问根节点,然后递归地对左子树进行先序遍历,最后递归地对右子树进行先序遍历。下面是对先序遍历的详细讲解:
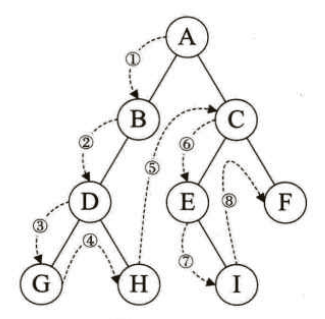
考虑以下二叉树:
9
/ \
7 16
/ \ \
3 14 26
/ / \
11 15 18先序遍历的顺序是从根节点开始,按照根-左-右的顺序访问节点。
访问根节点 9
- 从根节点开始,首先访问根节点9。
递归访问左子树 7
- 移至左子树,访问左子树的根节点7。
递归访问左子树 3
- 移至左子树的左子树,访问左子树的左子树的根节点3。
回溯到左子树 3,递归访问右子树 11
- 3没有右子树,回溯到7,然后访问7的右子树,即11。
回溯到左子树 7,递归访问右子树 14
- 7的左子树已经访问完,回溯到9,然后访问9的右子树的根节点14。
递归访问左子树 11
- 移至右子树的左子树,访问右子树的左子树的根节点11。
回溯到右子树 11,递归访问右子树 15
- 11没有左子树和右子树,回溯到14,然后访问14的右子树的根节点15。
回溯到右子树 14,递归访问右子树 18
- 14的左子树已经访问完,回溯到9,然后访问9的右子树的根节点18。
递归访问右子树 16
- 移至右子树的根节点16。
递归访问左子树 15
- 移至右子树的左子树,访问右子树的左子树的根节点15。
- 回溯到右子树 15,递归访问右子树 26
- 15没有左子树和右子树,回溯到16。
- 回溯到根节点 16,递归访问右子树 26
- 移至根节点的右子树,访问右子树的根节点26。
- 回溯到根节点 9,遍历完成
- 遍历完整个树。
最终的先序遍历序列是:9, 7, 3, 11, 16, 14, 15, 18, 26。
中序遍历
中序遍历是二叉树遍历的一种方式,它的遍历顺序是先递归地对左子树进行中序遍历,然后访问根节点,最后递归地对右子树进行中序遍历。下面是对中序遍历的详细讲解:
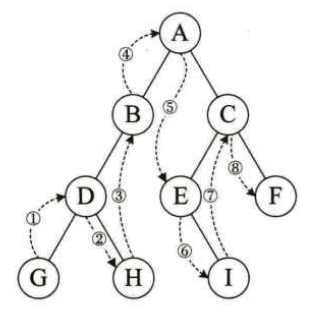
考虑以下二叉树:
9
/ \
7 16
/ \ \
3 14 26
/ / \
11 15 18中序遍历的顺序是从最左子节点开始,按照左-根-右的顺序访问节点。
递归访问左子树 3
- 从最左子节点3开始,递归访问左子树。
递归访问左子树 7
- 移至左子树的根节点7,递归访问左子树。
递归访问左子树 11
- 移至左子树的根节点11,递归访问左子树。
回溯到左子树 11,访问根节点 11
- 11没有左子树,回溯到7,然后访问7。
递归访问右子树 14
- 移至右子树的根节点14,递归访问左子树。
回溯到右子树 14,访问根节点 14
- 14没有左子树,回溯到3,然后访问3。
回溯到根节点 3,访问根节点 3
- 3没有右子树,回溯到9,然后访问9。
递归访问右子树 16
- 移至右子树的根节点16,递归访问左子树。
递归访问左子树 15
- 移至左子树的根节点15,递归访问左子树。
回溯到左子树 15,访问根节点 15
- 15没有左子树,回溯到16,然后访问16。
递归访问右子树 18
- 移至右子树的根节点18,递归访问左子树。
回溯到右子树 18,访问根节点 18
- 18没有左子树,回溯到9,中序遍历完成。
最终的中序遍历序列是:3, 7, 11, 14, 15, 16, 18, 26。
后序遍历
后序遍历是二叉树遍历的一种方式,它的遍历顺序是先递归地对左子树进行后序遍历,然后递归地对右子树进行后序遍历,最后访问根节点。下面是对后序遍历的详细讲解:
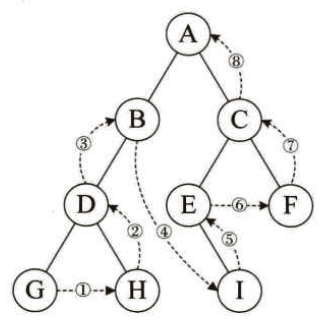
考虑以下二叉树:
9
/ \
7 16
/ \ \
3 14 26
/ / \
11 15 18后序遍历的顺序是从最左子节点开始,按照左-右-根的顺序访问节点。
递归访问左子树 3
- 从最左子节点3开始,递归访问左子树。
递归访问左子树 11
- 移至左子树的根节点11,递归访问左子树。
回溯到左子树 11,访问右子树 3
- 11没有右子树,回溯到3,然后访问3的右子树。
递归访问右子树 7
- 移至右子树的根节点7,递归访问左子树。
递归访问左子树 14
- 移至左子树的根节点14,递归访问左子树。
回溯到左子树 14,访问右子树 7
- 14没有右子树,回溯到7,然后访问7的右子树。
回溯到右子树 7,访问根节点 7
- 7的左右子树都访问完,回溯到根节点9。
递归访问右子树 15
- 移至右子树的根节点15,递归访问左子树。
回溯到右子树 15,访问右子树 14
- 15没有左子树,回溯到14,然后访问14的右子树。
回溯到右子树 14,访问根节点 14
- 14的左右子树都访问完,回溯到根节点9。
回溯到根节点 9,访问右子树 18
- 移至右子树的根节点18,递归访问左子树。
递归访问左子树 26
- 移至左子树的根节点26,递归访问左子树。
回溯到左子树 26,访问右子树 18
- 26没有右子树,回溯到18,然后访问18的右子树。
回溯到右子树 18,访问根节点 18
- 18的左右子树都访问完,回溯到根节点9。
回溯到根节点 9,遍历完成
- 遍历完整个树。
最终的后序遍历序列是:3, 11, 7, 15, 14, 18, 26, 16, 9。
顺序存储
二叉树的顺序存储是通过数组来表示二叉树的结构,具体的存储方式是按照二叉树的层次顺序,从上到下、从左到右,将每个节点按照这个顺序存储在数组中。
考虑以下二叉树:
1
/ \
2 3
/ \ \
4 5 6对这棵二叉树进行顺序存储,将节点按照层次顺序从上到下、从左到右依次存储在数组中。对应的数组表示为:
[1, 2, 3, 4, 5, #, 6]二叉树的高度
二叉树的高度是从根节点到最深叶子节点的最长路径的节点数。可以通过递归地计算左子树和右子树的高度,然后取较大值,再加上根节点的高度(1),得到整个二叉树的高度。
考虑以下二叉树:
9
/ \
7 16
/ \ \
3 14 26
/ / \
11 15 18二叉树的高度为4,因为最长路径为根节点到叶子节点18的路径。
链式存储
在链式存储结构中,每个节点包含一个数据域和两个指针域,分别指向左子树和右子树。通过这种方式,可以用指针来表示二叉树的节点之间的关系。以下是一个链式存储的二叉树的例子:
plaintext
1
/ \
2 3
/ \
4 5对应的链式存储结构:
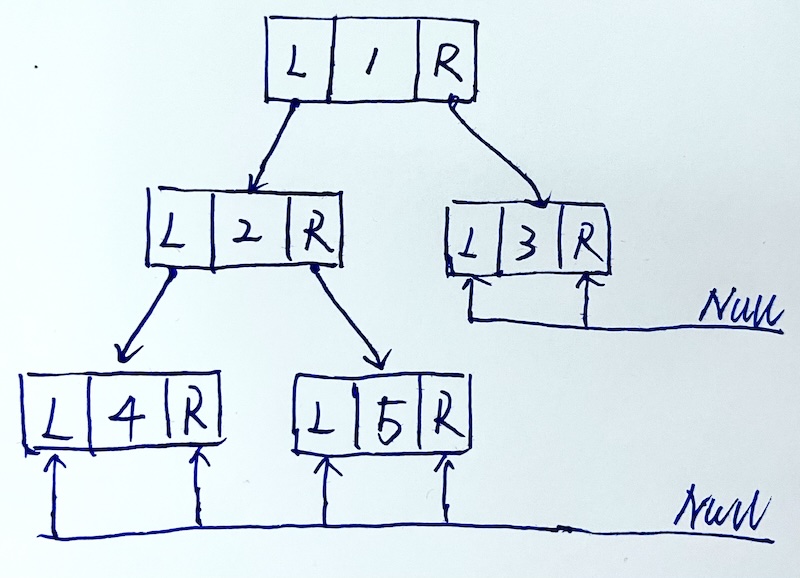
每个节点都包含一个数据域和两个指针域,例如:
- 结点1:数据域为1,左指针指向结点2,右指针指向结点3。
- 结点2:数据域为2,左指针指向结点4,右指针指向结点5。
- 结点3:数据域为3,左指针和右指针均为空。
- 结点4:数据域为4,左指针和右指针均为空。
- 结点5:数据域为5,左指针和右指针均为空。
在链式存储结构中,通过指针的连接关系表示了节点之间的层次和关联。这种结构更贴近二叉树的实际构造,更适用于动态的、频繁修改结构的场景。链式存储的优势在于它能够灵活地插入、删除节点,而不需要提前分配固定大小的存储空间。